Contr?le exact des limites des équations d'ondes semi-linéaires 1D par une approche constructive

L’équation des ondes modélise des phénomènes acoustiques et/ou vibratoires. Pour toute position \(y_0\) et vitesse \(y_1\) initiale, on cherche à montrer l’existence d’un contr?le frontière \(v\) tel que \(y(1,t)=v(t)\) agissant a l’une des extrémités de l’intervalle \((0,1)\) de fa?on à ce que la solution \(y\) atteigne un état cible prescrit \((z_0,z_1)\) à l’instant \(T\).

L’existence de tels contr?les est connue depuis un résultat de Zuazua en 1993, supposant que la nonlinearité \(f\) est localement lipschitz, continue et vérifie la condition de croissance a l’infini
\[\limsup_{\vert r\vert\to \infty} \vert f(r)\vert /(\vert r\vert \ln^{2}\vert r\vert)\leq \beta\] pour un réel \(\beta\) positif suffisamment petit.

La preuve non constructive est basée sur une linéarisation de l’équation et l’application d'un théorème de point fixe de Schauder.  

Le travail publié en 2023 dans le cadre du post-doctorat du chercheur de nationalité indienne Kuntal Bhandari financé par l’I-site apportent deux contributions nouvelles: d’une part, il propose une preuve simplifiée du résultat précédent tout en relaxant le caractère Lipschitz de la fonction \(f\): cette preuve s’appuie sur un opérateur de fixe différent ou toute la non linéarité est considérée comme un second membre de l‘équation.  D’autre part, en supposant une hypothèse de croissance à l’infini sur la dérivée de \(f\) de la forme 
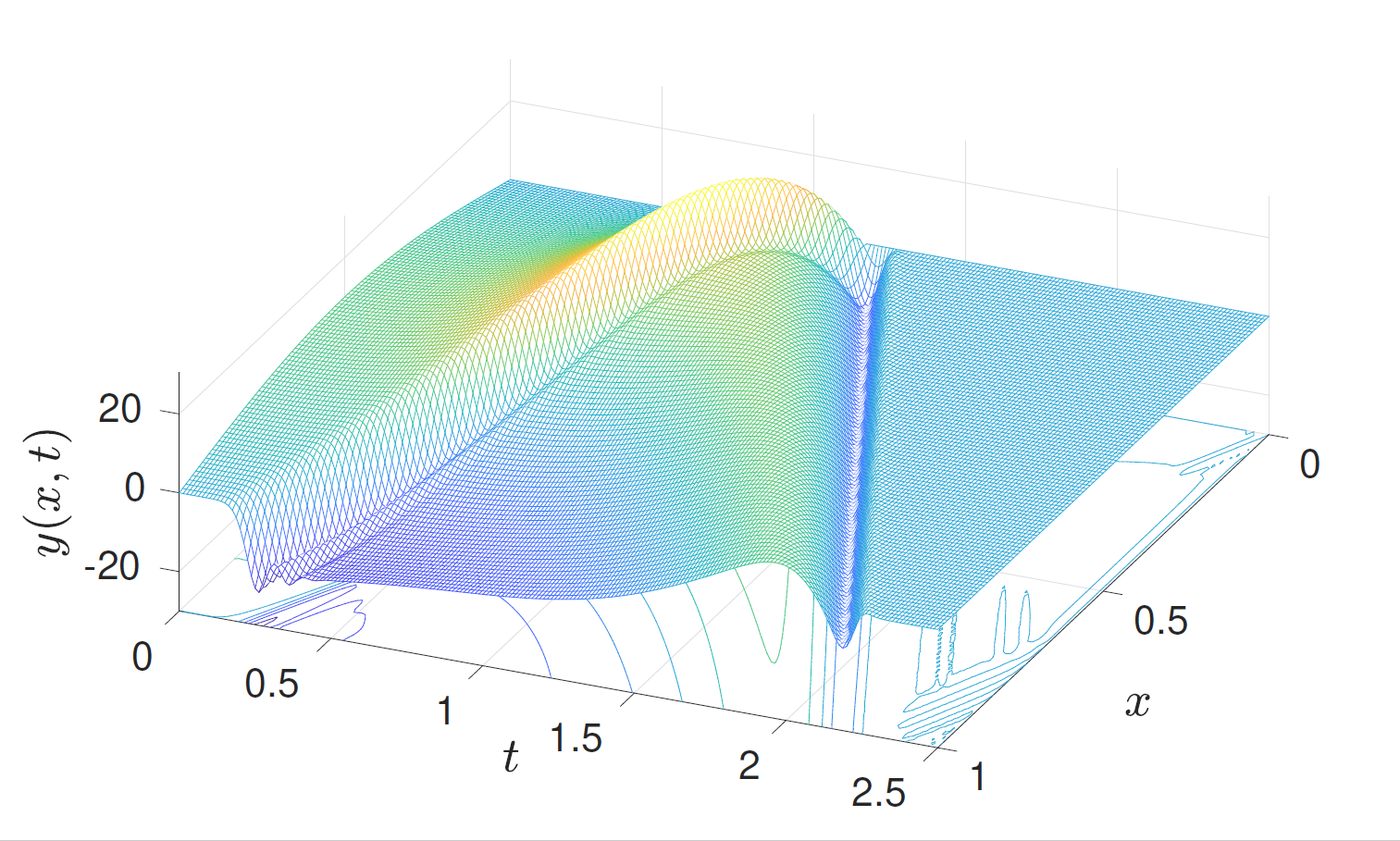
\[\limsup_{\vert r\vert\to \infty} \vert f^\prime(r)\vert/\ln^{3/2}\vert r\vert\leq \beta\] pour un réel \(\beta\) positif suffisamment petit, on montre que l’opérateur de point fixe est contractant menant à une méthode d’approximation de contr?les pour l’équation non linéarité initiale, basée sur les itérés de Picard de l’opérateur. La figure représente la solution contr?lée sur le domaine \((0,1)\times (0,T)\) avec \(T=2.5\), une non linéarité \(f(r)=-3r ln^{3/2}(1+\vert r\vert)\), un état initial \((y_0,y_1)=(10 \sin(\pi x),0)\) et un état cible \((z_0,z_1)=(0,0)\).  L’extension de ces résultats en toute dimension d'espace fait l’objet de la thèse de l’étudiante Sue Claret, démarrée en octobre 2022 au LMBP. 
 

D'après la publication de Bhandari, Kuntal; Lemoine, Jér?me; Münch, Arnaud, Exact boundary controllability of 1D semilinear wave equations through a constructive approach. Math. Control Signals Systems 35 (2023), no. 1, 77–123.